AVL Tree는 스스로 균형을 맞추는 이진탐색트리(BST)이다. 여기서 균형을 맞춘다는 것은 왼쪽/ 오른쪽 자식트리의 깊이 차이가 1을 넘지 않는다는 의미이다.
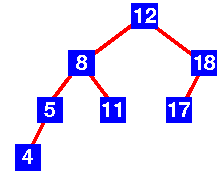
[그림1] AVL Tree
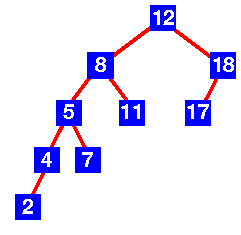
[그림 2] AVL Tree가 아님
위 [그림1, 2]는 AVL Tree의 성립 조건을 비교하는 예시이다.
[그림 1]의 경우는 모든 노드에서 자식노드들(왼쪽, 오른쪽)의 깊이 차이가 1을 넘지 않는다. 그런데 [그림 2]의 트리는 8과 18을 가진 노드에서 자식노드들의 깊이 차이가 1을 넘기 때문에 AVL Tree 조건을 성립하지 않는다.
왜 AVL Tree를 사용할까?
이진탐색트리의 작업들(검색, 삽입, 삭제 등)을 수행할 때 O(logN)의 시간이 소요된다. 하지만 한쪽으로 노드들이 쏠린 트리의 경우 수행시간이 O(N)으로 늘어나게 된다. 그래서 이진탐색트리의 작업들의 수행시간을 O(logN)으로 보장하기 위해서 트리의 좌/우 균형을 맞춰주는 자료구조로서 AVL Tree가 등장하게 되었다.
삽입
AVL Tree에 새로운 노드를 삽입 할 때, 트리의 균형이 맞도록 재조정 작업을 진행해야 한다.
트리의 균형을 맞출 때 지켜야 할 기준은 이진탐색트리(BST)와 동일하다.
T1, T2, T3는 루트노드 y 또는 x의 자식트리이다. (y는 왼쪽, x는 오른쪽 트리)
y x
/ \ Right Rotation / \
x T3 – – – – – – – > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
두 트리에서 지켜야 할 데이터 크기의 순서는 아래와 같다.
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
삽입의 순서
새로운 노드 w를 추가할 때, 순서는 아래와 같다.
- BST의 삽입 방법과 동일하게 w를 추가한다.
- 추가한 w로부터 불균형한 첫번째 노드를 찾는다. 찾은 불균형노드를 z라 한다. z에서 w로 이르는 과정의 자식노드를 y, 손자노드를 x라 한다.
- z을 루트로 하는 부분트리의 균형을 재배열한다. 재배열 작업 시 4가지 케이스가 존재하는데 다음과 같다.
a) y는 z의 왼쪽자식, x는 y의 왼쪽자식 (left left)
b) y는 z의 왼쪽자식, x는 y의 오른쪽자식 (left right)
c) y는 z의 오른쪽자식, x는 y의 오른쪽자식 (right right)
d) y는 z의 오른쪽자식, x는 y의 왼쪽자식 (right left)
4가지 케이스별로 재배열을 하는 방식이 다르다.
a) left left
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
b) left right
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
c) right right
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
d) right left
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
하나의 케이스만 예제로 살펴보도록 하자.
[그림 3]은 데이터 삽입 시 left left 형태로 구조가 이루어졌을 때, 재배열 하는 과정을 보여준다.
left left의 경우 오른쪽 회전을 통해 균형을 유지하도록 되어 있다.
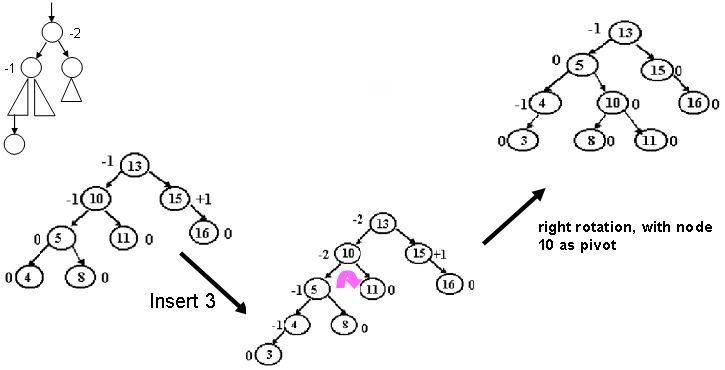
[그림 3] AVL Tree 삽입과정 예 (left left)
코드로 구현된 사항을 살펴보자.
public class AVLTree {
public class Node {
private int key, height;
private Node left, right;
public Node(int d) {
key = d;
height = 1;
}
}
private Node root;
// A utility function to get height of the tree
private int height(Node n) {
if (n == null) {
return 0;
}
return n.height;
}
// A utility function to right rotate subtree rooted with y
private Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
// Perform rotation
x.right = y;
y.left = T2;
// Update heights
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
// Return new root
return x;
}
// A utility function to left rotate subtree rooted with x
private Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = Math.max(height(x.left), height(x.right)) + 1;
y.height = Math.max(height(y.left), height(y.right)) + 1;
return y;
}
// Get Balance factor of Node n
private int getBalance(Node n) {
if (n == null) {
return 0;
}
return height(n.left) - height(n.right);
}
private Node insert(Node node, int key) {
if (node == null) {
return (new Node(key));
}
if (key < node.key) {
node.left = insert(node.left, key);
} else if (key > node.key) {
node.right = insert(node.right, key);
} else {
return node;
}
node.height = 1 + Math.max(height(node.left), height(node.right));
int balance = getBalance(node);
// If this node becomes unbalanced, then there are 4 cases
// left left case
if (balance > 1 && key < node.left.key) {
return rightRotate(node);
}
// right right case
if (balance < -1 && key > node.right.key) {
return leftRotate(node);
}
// left right case
if (balance > 1 && key > node.left.key) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// right left case
if (balance < -1 && key < node.right.key) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
private void inOrder(Node node) {
if (node != null) {
inOrder(node.left);
System.out.println(node.key + " ");
inOrder(node.right);
}
}
public static void main(String[] args) {
AVLTree tree = new AVLTree();
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 20);
tree.root = tree.insert(tree.root, 30);
tree.root = tree.insert(tree.root, 40);
tree.root = tree.insert(tree.root, 50);
tree.root = tree.insert(tree.root, 25);
/* The constructed AVL Tree would be
30
/ \
20 40
/ \ \
10 25 50
*/
tree.inOrder(tree.root);
}
}
이번 블로그에 빠져있는 AVL 삭제에 대한 내용은 다음에 살펴보도록 하자.
[참고]
반응형
'Algorithm' 카테고리의 다른 글
| Raft 알고리즘 요약 (0) | 2023.03.30 |
|---|---|
| AVL Tree (2) - 삭제 (0) | 2017.08.25 |
| [algospot] 조세푸스 문제 (연결리스트) (0) | 2017.08.03 |
| [Euler] Highly divisible triangular number (0) | 2016.03.25 |
| [분할정복] 카라츠바 알고리즘 (0) | 2014.06.21 |